We explore a new class of diffusion models based on the transformer architecture. We train latent diffusion models, replacing the commonly-used U-Net backbone with a transformer that operates on latent patches. We analyze the scalability of our Diffusion Transformers (DiTs) through the lens of forward pass complexity as measured by Gflops. We find that DiTs with higher Gflops—through increased transformer depth/width or increased number of input tokens—consistently have lower FID. In addition to good scalability properties, our DiT-XL/2 models outperform all prior diffusion models on the class-conditional ImageNet 512×512 and 256×256 benchmarks, achieving a state-of-the-art FID of 2.27 on the latter.

Diffusion x Transformers

Diffusion models have achieved amazing results in image generation over the past year. Almost all of these models use a convolutional U-Net as a backbone. This is sort of surprising! The big story of deep learning over the past couple of years has been the dominance of transformers across domains. Is there something special about the U-Net—or convolutions—that make them work so well for diffusion models?

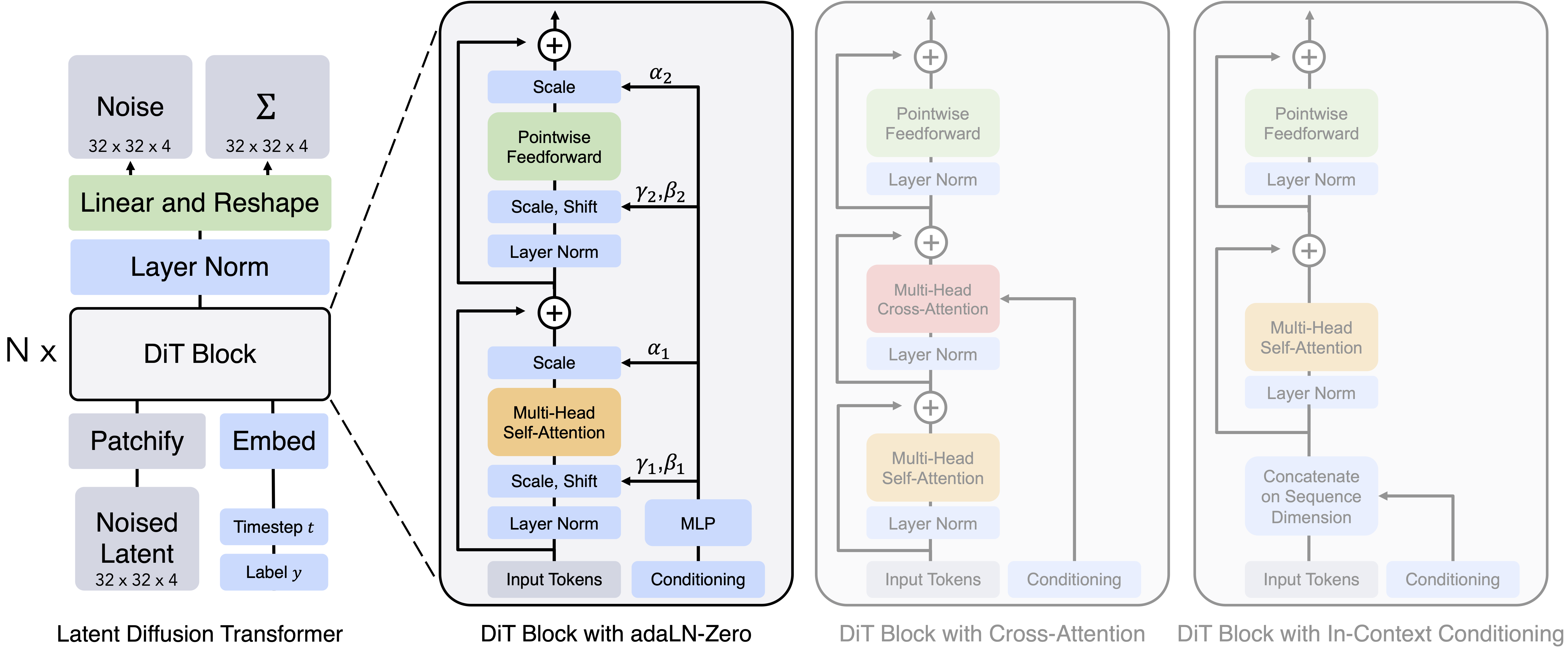
In this paper, we replace the U-Net backbone in latent diffusion models (LDMs) with a transformer. We call these models Diffusion Transformers, or DiTs for short. The DiT architecture is very similar to a standard Vision Transformer (ViT), with a few small, but important, tweaks. Diffusion models need to process conditional inputs, like diffusion timesteps or class labels. We experimented with a few different block designs to inject these inputs. The one that works best is a ViT block with adaptive layer norm layers (adaLN). Importantly, these adaLN layers also modulate the activations immediately prior to any residual connections within the block, and are initialized such that each ViT block is the identity function. Simply changing the mechanism for injecting conditional inputs makes a huge difference in terms of FID. This change was the only one we needed to get good performance; otherwise, DiT is a fairly standard transformer model.

Scaling DiT

Scaling-up the DiT model significantly increases sample quality. — Visualizing the effects of scaling-up DiT. We generated images from all 12 of our DiT models at 400K training steps using identical sampling noise. More compute-intensive DiT models have significantly-higher sample quality.

Transformers are known to scale well in a variety of domains. How about as diffusion models? We scale DiT along two axes in this paper: model size and number of input tokens.

Scaling model size. We tried four configs that differ by model depth and width: DiT-S, DiT-B, DiT-L and DiT-XL. These model configs range from 33M to 675M parameters and 0.4 to 119 Gflops. They are borrowed from the ViT literature which found that jointly scaling-up depth and width works well.

Scaling tokens. The first layer in DiT is the patchify layer. Patchify linearly embeds each patch in the input image (or, in our case, the input latent), converting them into transformer tokens. A small patch size corresponds to a large number of transformer tokens. For example, halving the patch size quadruples the number of input tokens to the transformer, and thus at least quadruples the total Gflops of the model. Although it has a huge impact on Gflops, note that patch size does not have a meaningful effect on model parameter counts.

For each of our four model configs, we train three models with latent patch sizes of 8, 4 and 2 (a total of 12 models). Our highest-Gflop model is DiT-XL/2, which uses the largest XL config and a patch size of 2.

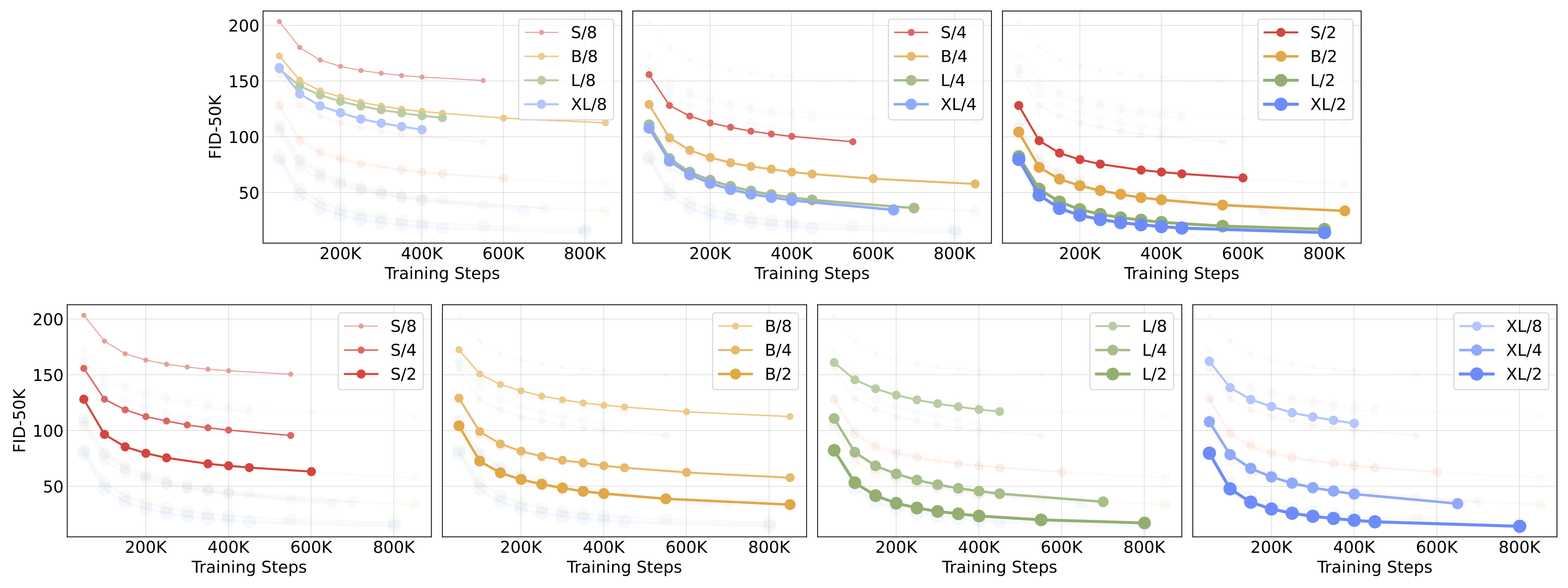
Scaling both model size and the number of input tokens substantially improves DiT's performance, as measured by Fréchet Inception Distance (FID). As has been observed in other domains, compute—not just parameters—appears to be the key to obtaining better models. For example, while DiT-XL/2 obtains excellent FID values, XL/8 performs poorly. XL/8 has slightly more parameters than XL/2 but much fewer Gflops. We also find that our larger DiT models are compute-efficient relative to smaller models; the larger models require less training compute to reach a given FID than smaller models (see the paper for details).

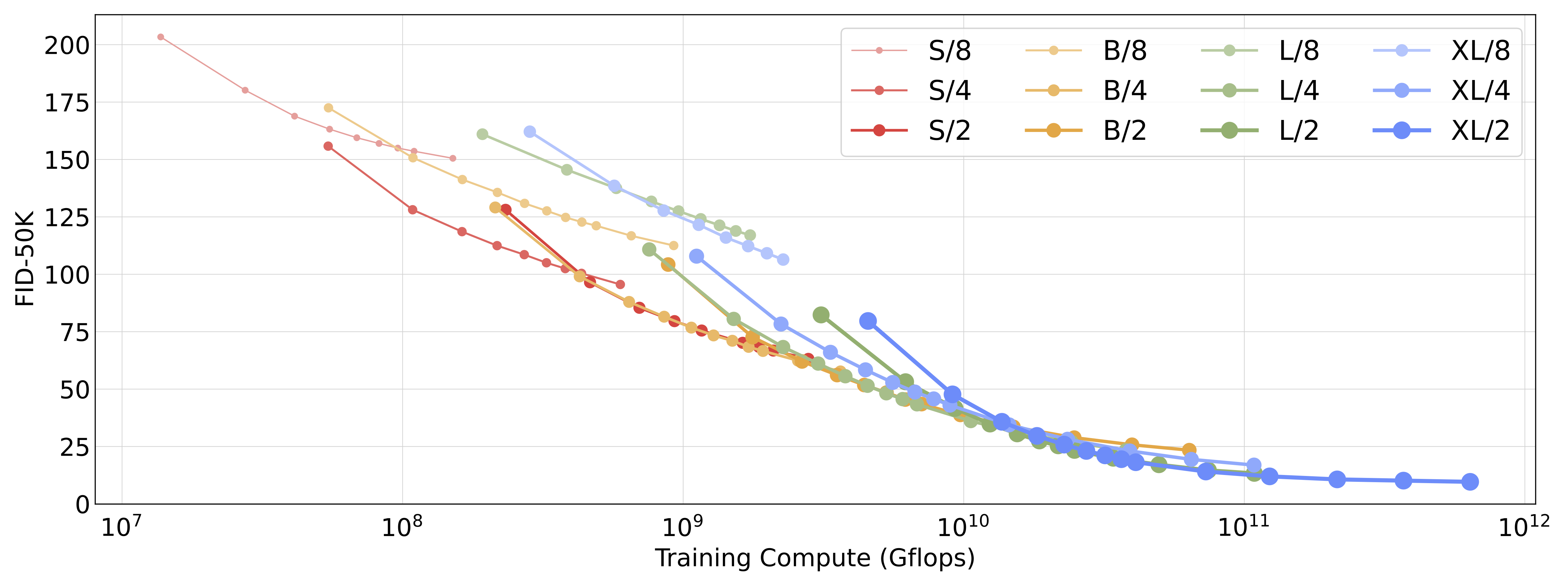
Following our scaling analysis, DiT-XL/2 is clearly the best model when trained sufficiently long. We'll focus on XL/2 for the rest of this post.

Comparison to State-of-the-Art Diffusion Models

Samples from our state-of-the-art DiT-XL/2 model. — Selected samples from our DiT-XL/2 models trained at 512x512 resolution (top row) and 256x256 resolution (bottom). Here, we used classifier-free guidance scales of 6.0 for the 512 model and 4.0 for the 256 model.

We trained two versions of DiT-XL/2 at 256x256 and 512x512 resolution on ImageNet for 7M and 3M steps, respectively. When using classifier-free guidance, DiT-XL/2 outperforms all prior diffusion models, decreasing the previous best FID-50K of 3.60 achieved by LDM (256x256) to 2.27; this is state-of-the-art among all generative models. XL/2 again outperforms all prior diffusion models at 512x512 resolution, improving the previous best FID of 3.85 achieved by ADM-U to 3.04.

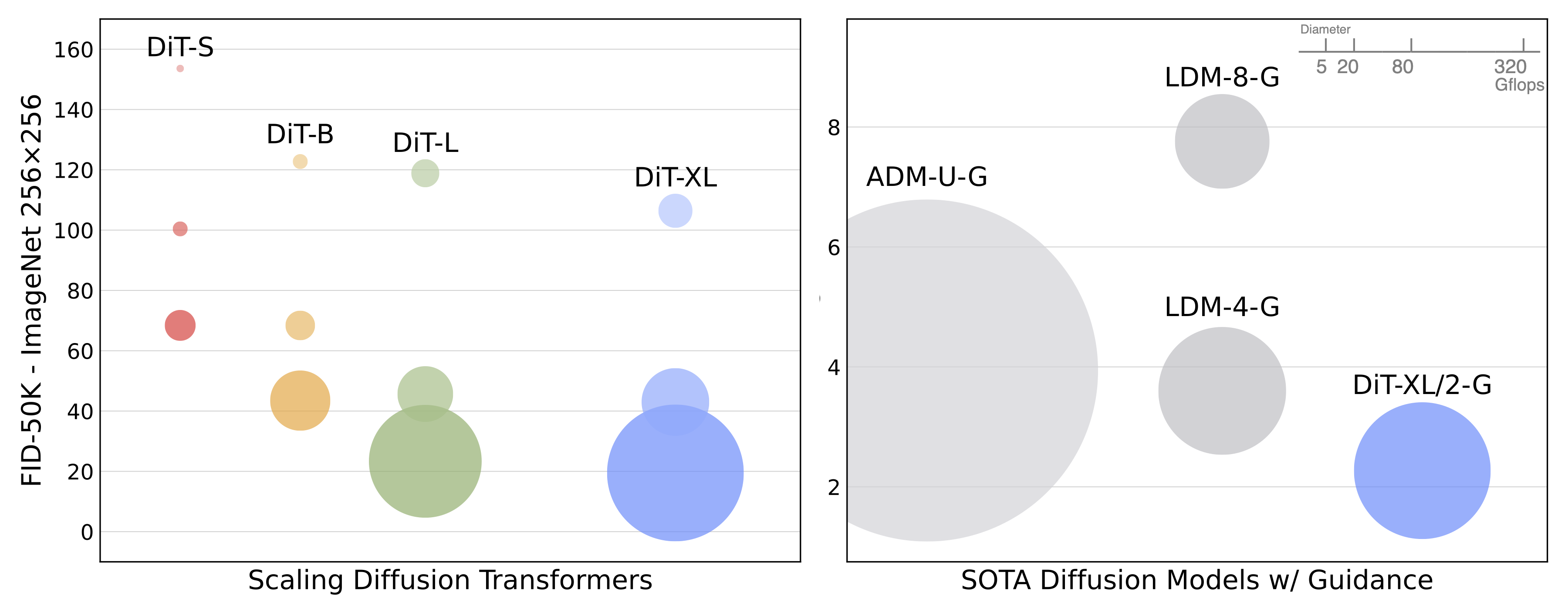
In addition to obtaining good FIDs, the DiT model itself remains compute-efficient relative to baselines. For example, at 256x256 resolution, the LDM-4 model is 103 Gflops, ADM-U is 742 Gflops and DiT-XL/2 is 119 Gflops. At 512x512 resolution, ADM-U is 2813 Gflops whereas XL/2 is only 525 Gflops.

Walking Through Latent Space

Finally, we show some latent walks for DiT-XL/2. We slerp through several different selections of initial noise, using the deterministic DDIM sampler to generate each intermediate image.

Walking through the latent space of DiT-XL/2 (256x256). We use a classifier-free guidance scale of 4.0.
[Uncompressed]

We can also walk through the label embedding space of DiT. For example, we can linearly interpolate between the embeddings for many dog breeds as well as the "tennis ball" class.

Walking through DiT-XL/2's (512x512) learned label embedding space. We interpolate dog breeds and "tennis ball" (first column), ocean marine life classes (second), natural settings (third) and bird species (fourth).
[Uncompressed]

As shown in the left-most column above, DiT can generate animal and object hybrids by simply interpolating between embeddings (similar to the dog-ball hybrid from BigGAN!).

Generative modeling has truly progressed.

BibTeX

@article{Peebles2022DiT,
  title={Scalable Diffusion Models with Transformers},
  author={William Peebles and Saining Xie},
  year={2022},
  journal={arXiv preprint arXiv:2212.09748},
}